2 Stress
Introduction
Click to expand
Having reviewed static equilibrium in Chapter 1, we now know how to find the internal loads in a body using equilibrium. When determining whether a body can resist the loads applied to it, the internal load is only part of the solution. The dimensions of the body and the inherent properties of the material it is made from are also important.
In this chapter we’ll explore the concept of stress, which can help us determine whether an object will physically break when subjected to a load. We’ll cover average normal stress (stress perpendicular to the cross-section) in Section 2.1 and average shear stress (stress parallel to the cross-section) in Section 2.2. We’ll then discuss bearing stress (the stress between two bodies in contact with each other) in Section 2.3 and finish with the average normal and shear stresses on an inclined cross-section in Section 2.4.
2.1 Average Normal Stress
Click to expand
Average normal stress is defined as the internal normal force divided by the cross-sectional area of the body. It is given the Greek letter sigma (σ). Stress increases as the force increases or as the cross-sectional area decreases.
\[ \boxed {\sigma=\frac{N}{A}} \tag{2.1}\]
𝜎 = Average normal stress [Pa, psi]
N = Internal normal force [N, lb]
A = Cross-sectional area [m2, in.2]
As such the SI units of stress are N/m2, more commonly referred to as the Pascal (Pa) where 1 Pa = 1 N/m2. The US customary units for stress are lb/in2, commonly written as psi. Since stresses can get very large, it is common to use prefixes such as kilo (k) and mega (M) to represent 103 and 106 respectively. A stress of 15,000,000 Pa is written as 15 MPa. A stress of 35,000 psi is written as 35 ksi.
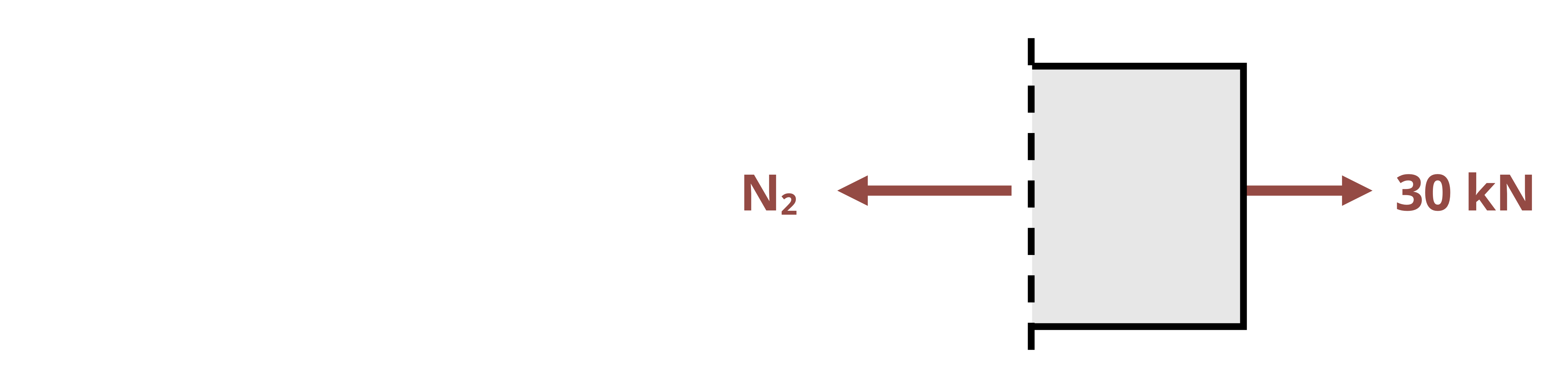
Normal stress occurs perpendicular to the cross-section and so is associated with either a pulling or pushing motion (Figure 2.1). Normal forces that pull on a cross-section are known as tensile forces and create a tensile normal stress. Normal forces that push on a cross-section are known as compressive forces and create a compressive normal stress. The normal stress calculated above is really an average normal stress as the force is distributed over the cross-section, but we generally simplify this to a concentrated force that creates the same normal stress at every point on the cross-section (Figure 2.2).
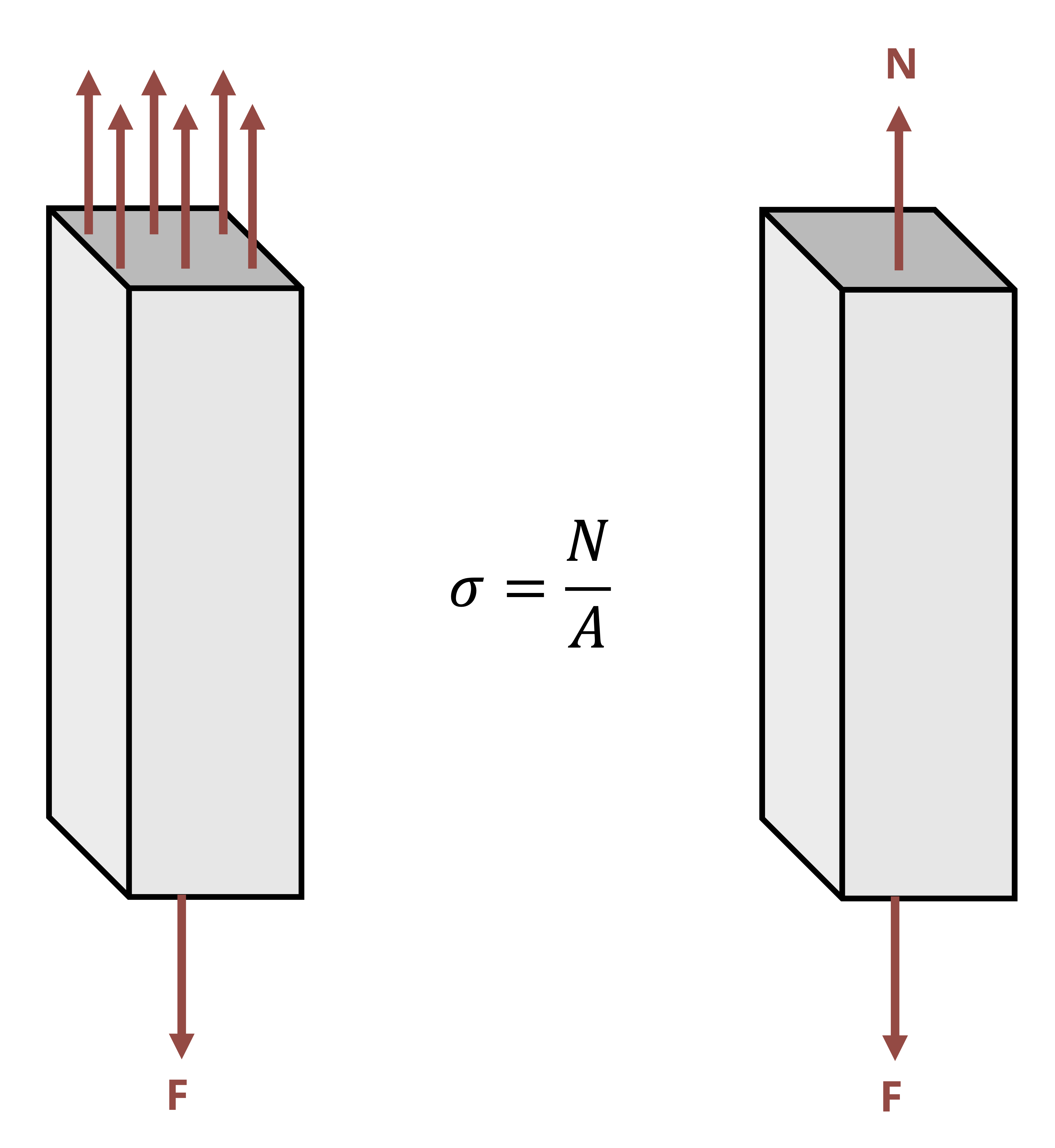
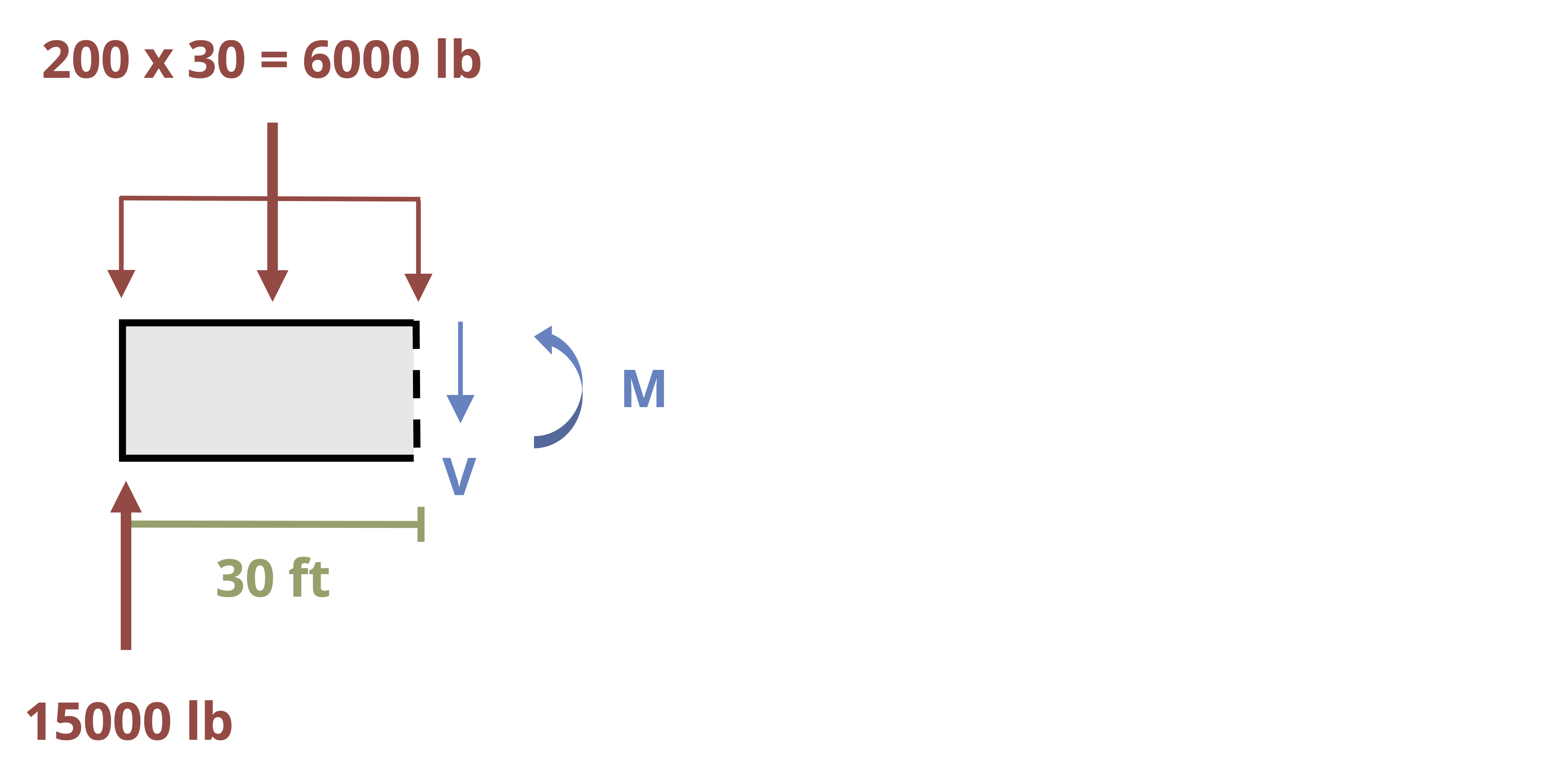
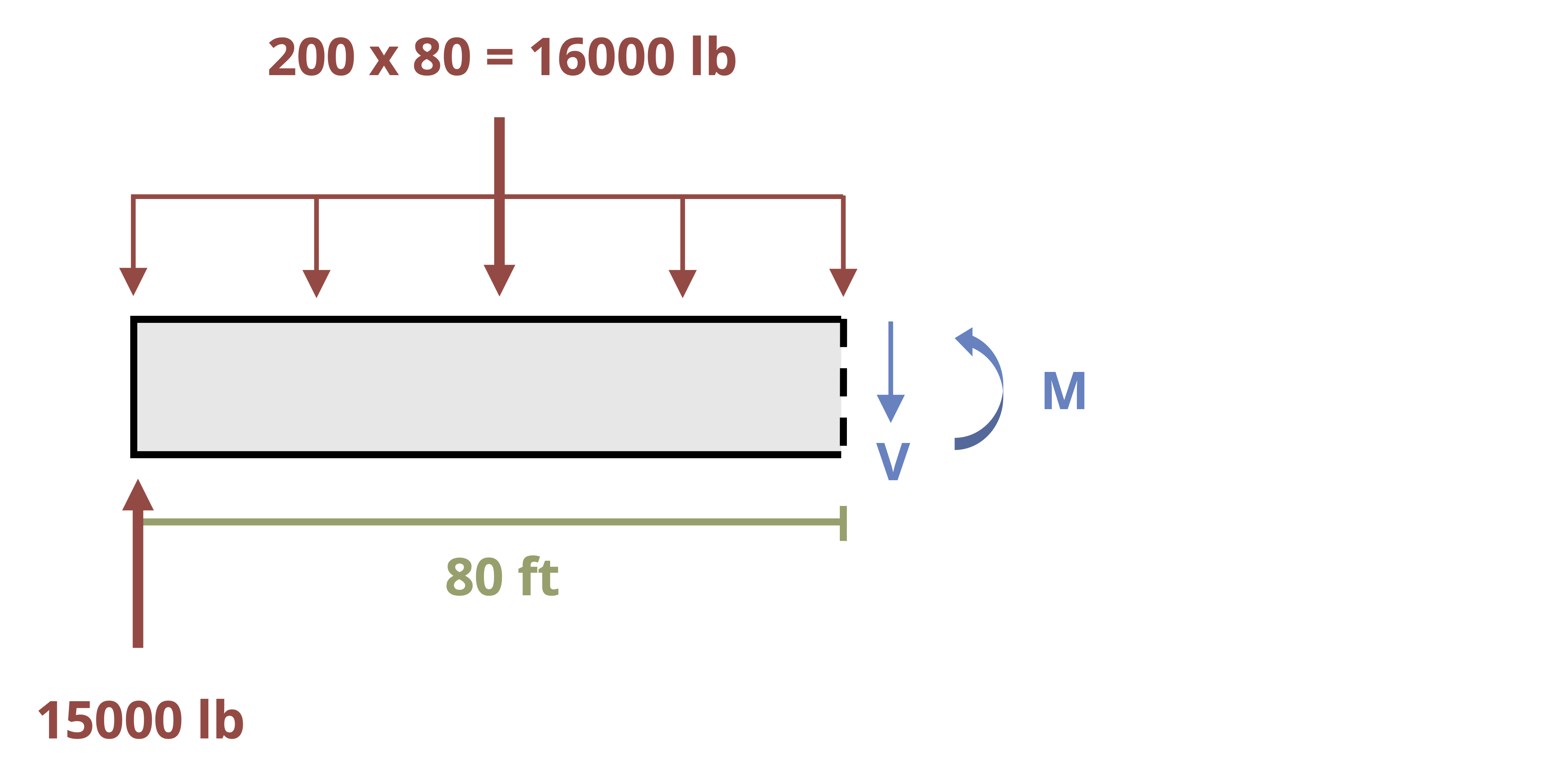
The internal normal force in a body can be found through the method of equilibrium as reviewed in Section 1.2. See Example 2.1 for a demonstration.
Example 2.1
The support column will be subjected to a compressive force F = 65 kips.
The diameter of the column is 4 inches. Determine the average normal stress in the column.
The column is to be made of concrete with an allowable compressive stress of 4 ksi. For the same force F = 65 kips, determine the required diameter of the column so that the average normal stress does not exceed 4 ksi.
- Cut a cross-section through the column and draw a free body diagram. Although it is clear in this case that the internal load will be 65 kips, it is best to get in the habit of writing out equilibrium equations.
\[ \sum F_y= N-65{~kips}=0 \]
The column has a circular cross-section of area \(A=\pi(2)^2=4 \pi{~in.}^2\).
The average normal stress can now be found from:
\[ \sigma=\frac{N}{A}=\frac{65{~kips}}{4 \pi{~in.}^2}=5.17{~ksi} \]
- Use the average normal stress equation again, but this time the stress is known to be 4 ksi. The loading has not changed so the internal normal force will still be 65 kips.
\[ \sigma=\frac{N}{A} \rightarrow A=\frac{N}{\sigma}=\frac{65{~kips}}{4{~ksi}}=16.25 {~in}^2 \]
Since \(A=\pi r^2\) we can find \(r=\sqrt{\frac{A}{\pi}}=\sqrt{\frac{16.25{~in.}^2}{\pi}}=2.27{~in}\).
Then \(d=2 r=2 * 2.27{~in.}=4.55{~in.}\)
Note that this is the minimum required diameter to ensure the average normal stress does not exceed 4 ksi. If the diameter is any smaller than this, the stress will exceed the 4 ksi limit.
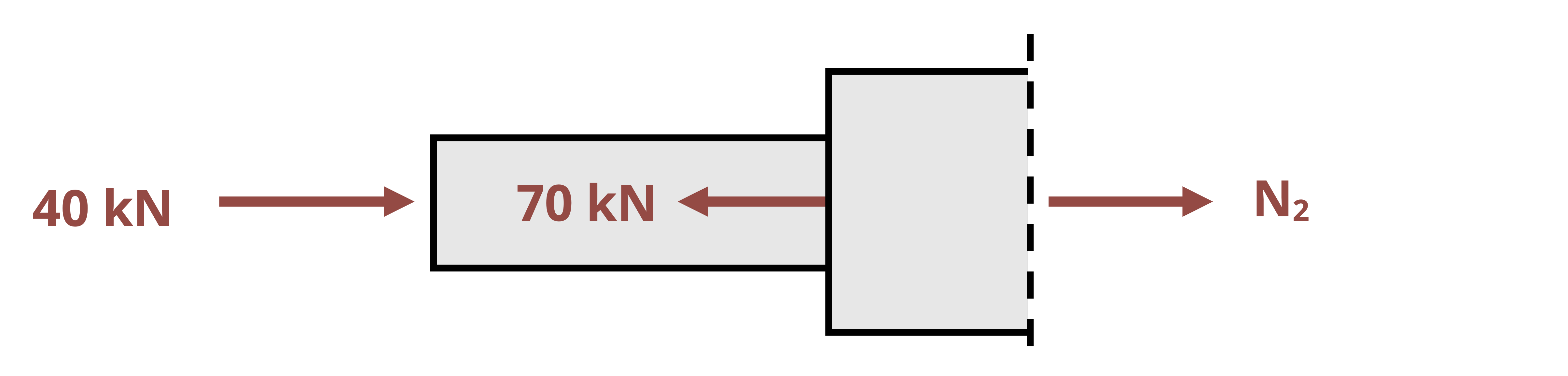
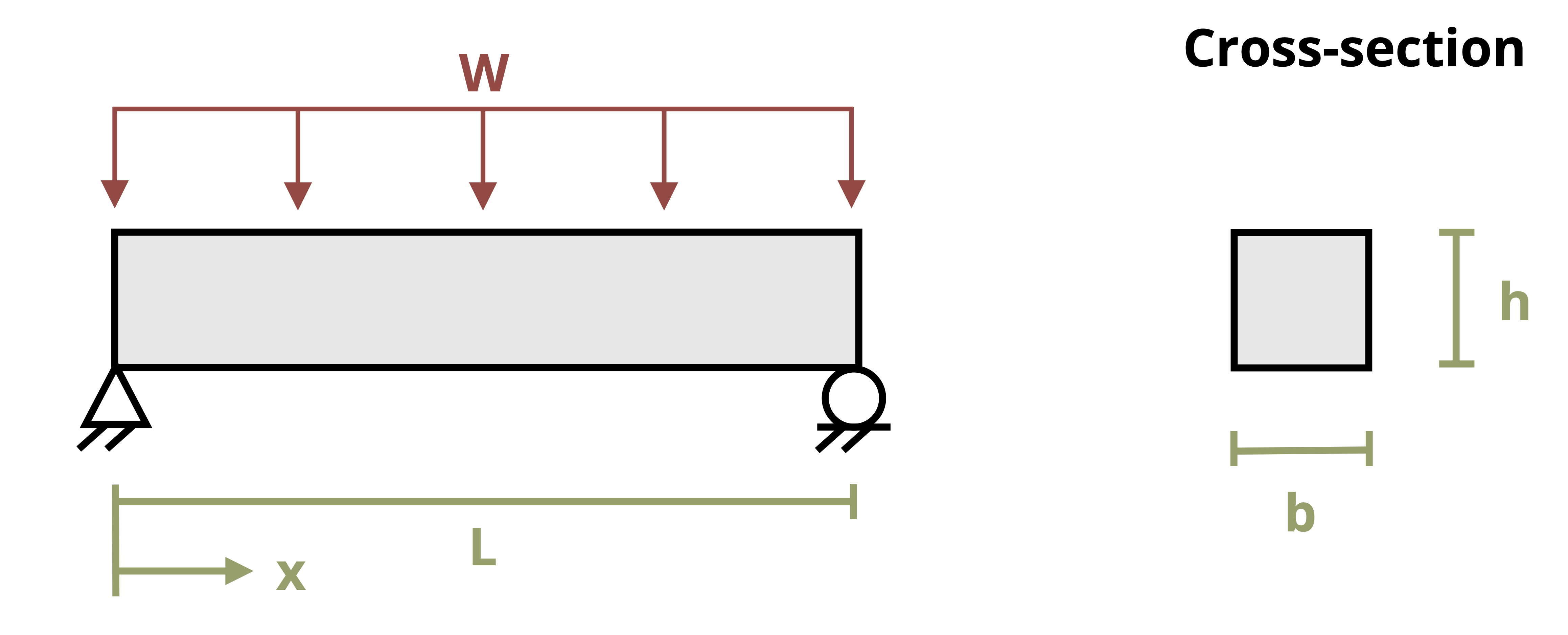
Sometimes the loading or cross-sectional area of the body will change, resulting in a change in stress. In these cases the stress can be calculated separately in each segment of the body by first finding the internal load in each segment and then dividing the internal load by the cross-sectional area of the respective segment. Different parts of the body may experience different stresses. Generally the highest stress is of most importance as that is the stress that typically determines whether the body will break. Because we do not know in advance where the largest stress is, however, it is typically necessary to calculate the stress at each different cross-section in order to determine the highest stress. See Example 2.2 for a demonstration.
Example 2.2
Two hollow pipes are welded together as shown. Pipe (1) has an outer diameter of 70 mm and an inner diameter of 40 mm while pipe (2) has an outer diameter of 110 mm and an inner diameter of 60 mm. Forces are applied at the end of each pipe and at the weld, where F1 = 40 kN, F2 = 70 kN, and F3 = 30 kN. Determine the average normal stress in each pipe.
We can calculate average normal stress using \(\sigma=\frac{N}{A}\) so we will need to find the area of each pipe and the normal force in each pipe. This can be done in any order. Starting with the areas:
\[ \begin{aligned} & A_1=\pi\left(0.035^2-0.02^2\right)=0.00259{~m}^2 \\ & A_2=\pi\left(0.055^2-0.03^2\right)=0.00668{~m}^2 \end{aligned} \]
The internal loads can be found by cutting a cross-section through each pipe, drawing a free body diagram, and writing an equilibrium equation.
\[ \begin{aligned} &\sum F_x=40{~kN}-N_1=0 \quad \rightarrow \quad N_1=40{~kN} \\ &\sum F_x=40{~kN}-70{~kN}+N_2=0 \quad \rightarrow \quad N_2=30{~kN} \end{aligned} \]
Note that we may choose to draw the internal load in either tension or compression. The answer must be compared to the free body diagram. A positive answer from the equilibrium equation indicates that the direction drawn on the free body diagram was correct. Although both answers here were positive, it can be seen in the free body diagrams that N1 was drawn in compression and N2 was drawn in tension. These positive answers indicate that the drawings are correct. N1 is 40 kN in compression and N2 is 30 kN in tension.
Note also that it is acceptable to draw a free body diagram of either side of the cross-section. This will not change the result. Perhaps it would have been easier to draw the right-hand-side of section 2.
\[ \sum F_x=30{~kN}+N_2=0 \quad \rightarrow \quad N_2=30{~kN} \]
We again find that N2 is 30 kN in tension. You may always choose to draw either side of a cross-section. Make sure to include everything to that side of your cut, all the way to the end of the structure (e.g. do not stop at the weld).
Now that the areas and internal loads are known we can calculate the internal normal stresses.
\[ \begin{gathered} \sigma_1=\frac{N_1}{A_1}=\frac{-40,000{~N}}{0.00259{~m}^2}=-15.4{~MPa} \\ \sigma_2=\frac{N_2}{A_2}=\frac{30,000{~N}}{0.00668{~m}^2}=4.49{~MPa} \end{gathered} \]
2.2 Average Shear Stress
Click to expand
Average shear stress is defined as the internal shear force divided by the cross-sectional area of the body. While normal forces (and therefore normal stresses) occur when a body is under tension or compression, shear forces (and therefore shear stresses) occur when a force is tangentially applied parallel to the cross-section, resulting in a sliding motion (Figure 2.3).
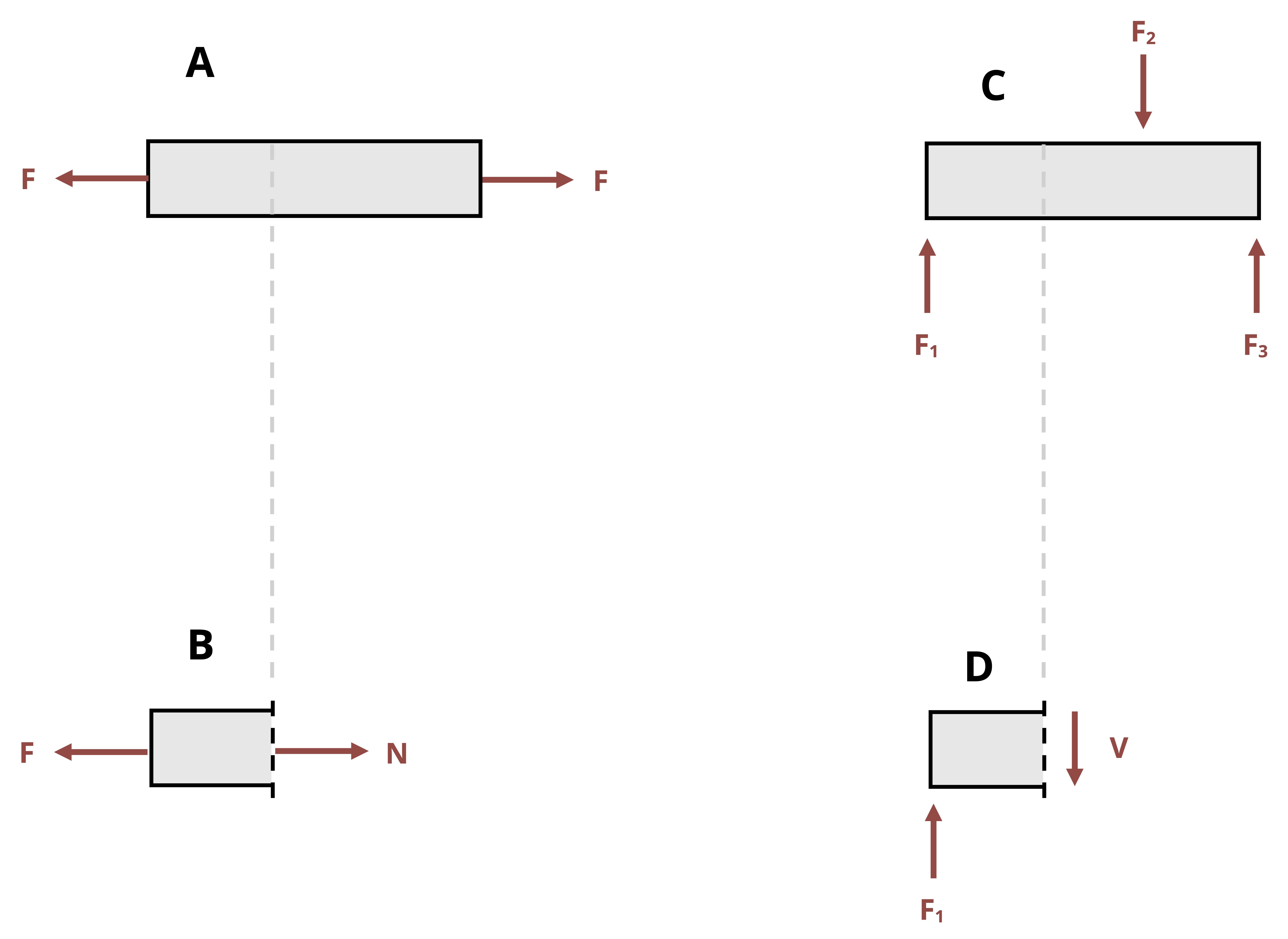
Although the basic definition of average normal stress and average shear stress is the same (force divided by area) there are some differences. To quickly differentiate which stress we are talking about, shear stress is denoted by the Greek letter tau (τ).
\[ \boxed{\tau=\frac{V}{A}} \tag{2.2}\]
τ = Average shear stress [Pa, psi]
V = Internal shear force [N, lb]
A = Cross-sectional area [m2, in.2]
Like normal force, internal shear force can be found by cutting a cross-section through the body, drawing a free body diagram, and applying equilibrium equations. See Example 2.3 for a demonstration.
Example 2.3
A bridge spans a gap of L = 150 ft. The roadway may be considered simply supported and has a rectangular cross-section of base b = 10 in. and height h = 6 in. It is subjected to a uniform distributed load of w = 200 lb/ft. Determine the magnitude of the average shear stress in the cross-section at x = 30 ft and x = 80 ft.
Average shear stress can be calculated from \(\tau=\frac{V}{A}\). The cross-sectional area is \(A=10{~in.}*6{~in.}=60{~in.}^2\)
The reactions at the support can be found by converting the distributed load into a statically equivalent concentrated load. This load will be equal to \(F=200{~lb/ft}*150{~ft}=30000{~lb}\) and will be located at the center of the bridge. Since the loading is symmetric, each support will support half of this load, or 15000 lb each.
The internal shear force can be found by cutting a cross-section through the point of interest, drawing a free body diagram, and applying equilibrium equations. Remember to include the internal loads V and M, and to again convert the distributed load into a statically equivalent concentrated load over this portion of the bridge.
At x = 30 ft:
\[ \sum F_y=15,000{~lb}-6,000{~lb}-V=0 \quad \rightarrow \quad V=9,000{~lb} \]
Note that an internal bending moment is also necessary in order to maintain equilibrium. We could find M by summing moments about any point, but it is not needed in order to solve this problem.
The shear stress can now be calculated.
\[ \tau=\frac{V}{A}=\frac{9,000{~lb}}{60{~in.}^2}=150{~psi} \]
At x = 80 ft:
\[ \sum F_y=15,000{~lb}-16,000{~lb}-V=0 \quad \rightarrow \quad V=-1,000{~lb} \]
Note that the negative sign here simply indicates that V is acting in the opposite direction of that drawn in the free body diagram. It can be discarded here as we are calculating the magnitude of the average shear stress at each point.
\[ \tau=\frac{V}{A}=\frac{1,000{~lb}}{60{~in.}^2}=16.7{~psi} \]
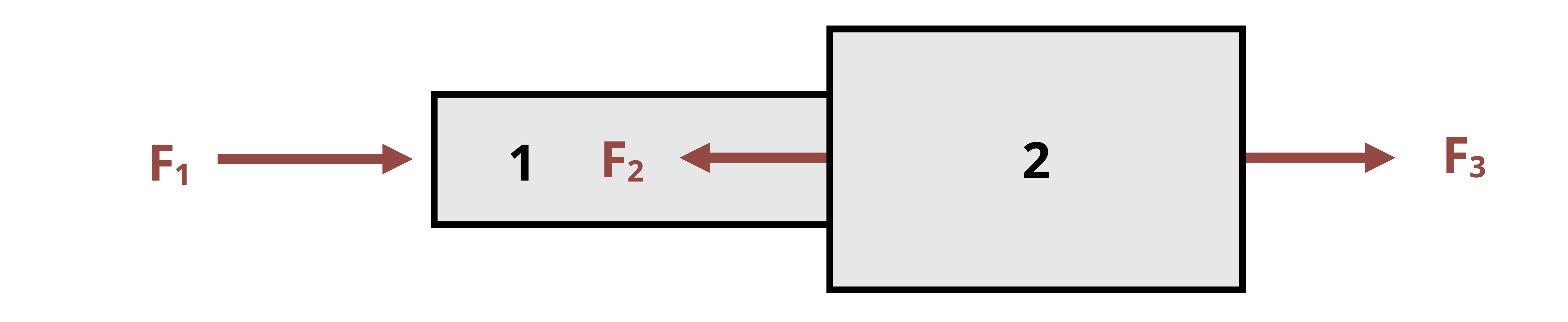
Shear stresses are common in both members of a structure and also in the fasteners between members. Depending on how these connections are formed we may see multiple shear planes. It is very important to correctly identify the internal force in the body. Figure 2.4 demonstrates the difference between single and double shear configurations for a pinned joint and the effects on internal shear force. See Example 2.4 for an example where double shear occurs.
Example 2.4
A pin made of a tin alloy with an allowable shear stress of 3 ksi is used to connect a footrest to the frame of a motorcycle. When in motion, the footrest supports a load of 200 lb which is transferred to the pin. Determine the required diameter of the pin such that the stress will not exceed 5 ksi.
.png)
2.3 Bearing Stress
Click to expand
Bearing stress is similar to normal stress, except that it occurs at the contact area between two bodies instead of within a single body. Bearing stress is calculated with the average normal stress equation, where the cross-sectional area is the contact area between the two bodies (Figure 2.5).
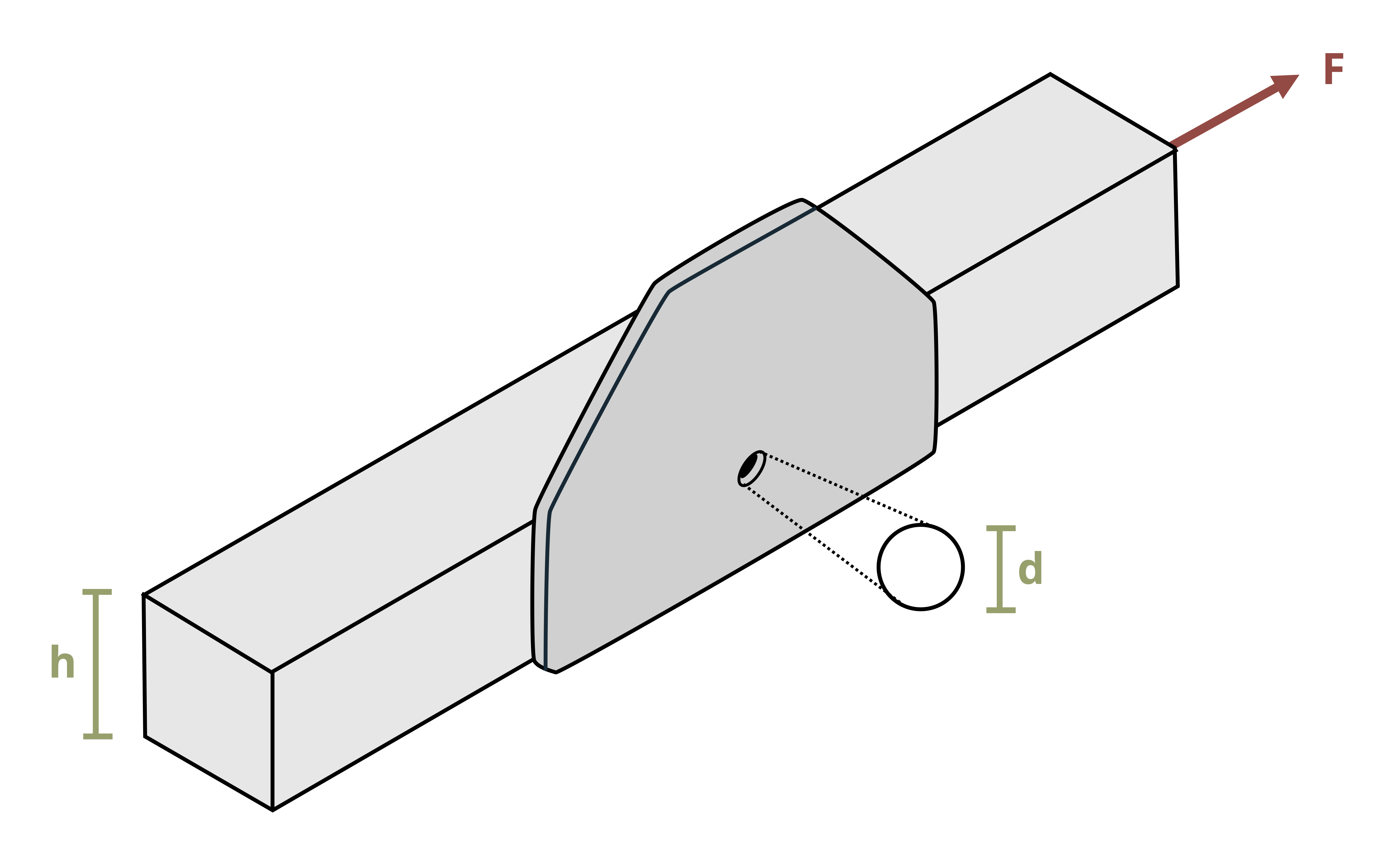
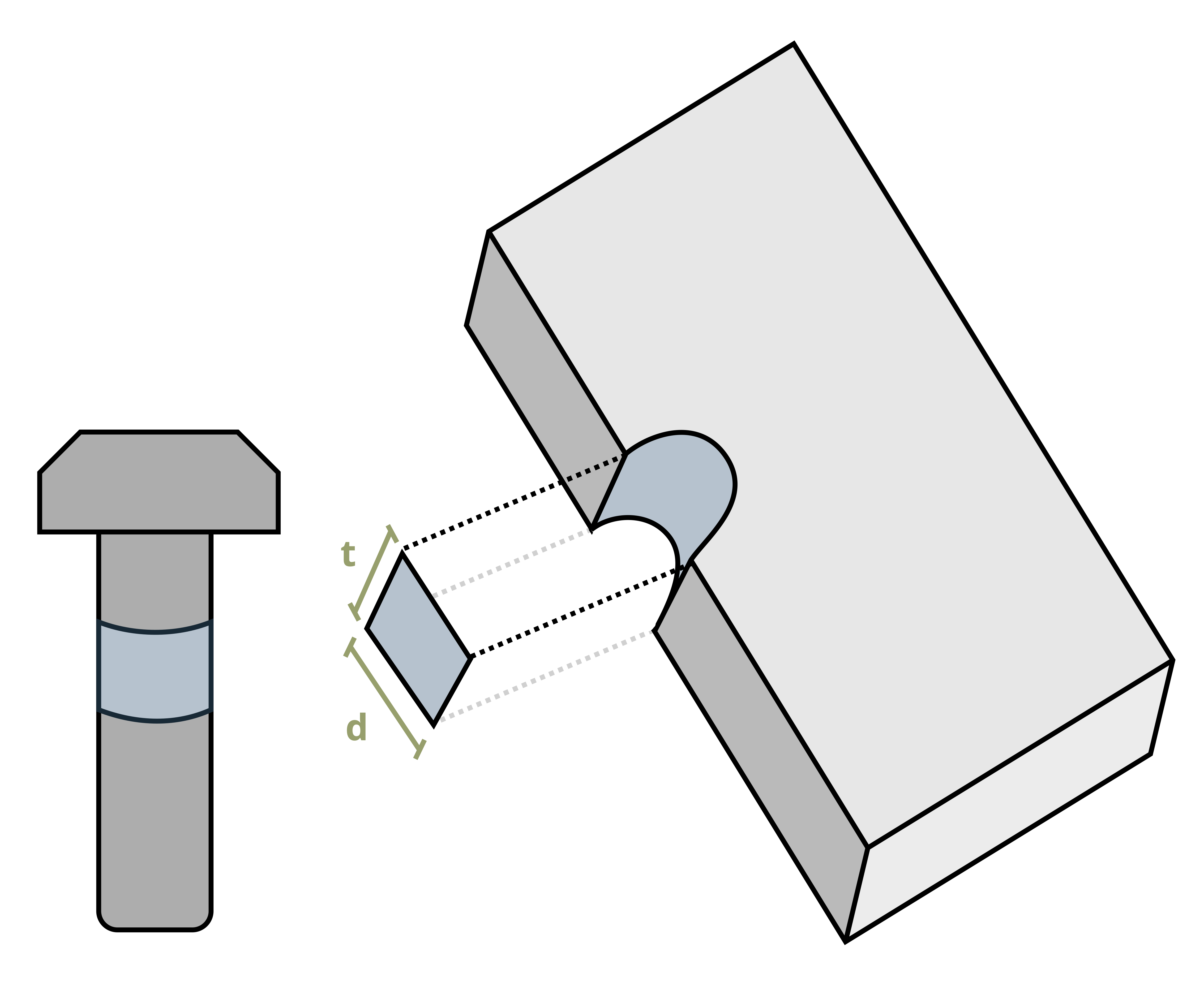
One common situation is contact between two curved edges, such as the bolt in Figure 2.6. In this situation it is common to use the projected contact area between the curved surfaces, which forms a rectangle of base d and height t. This greatly simplifies the calculation, but again represents an average value for the contact or bearing stress.
2.4 Stress on an Inclined Plane
Click to expand
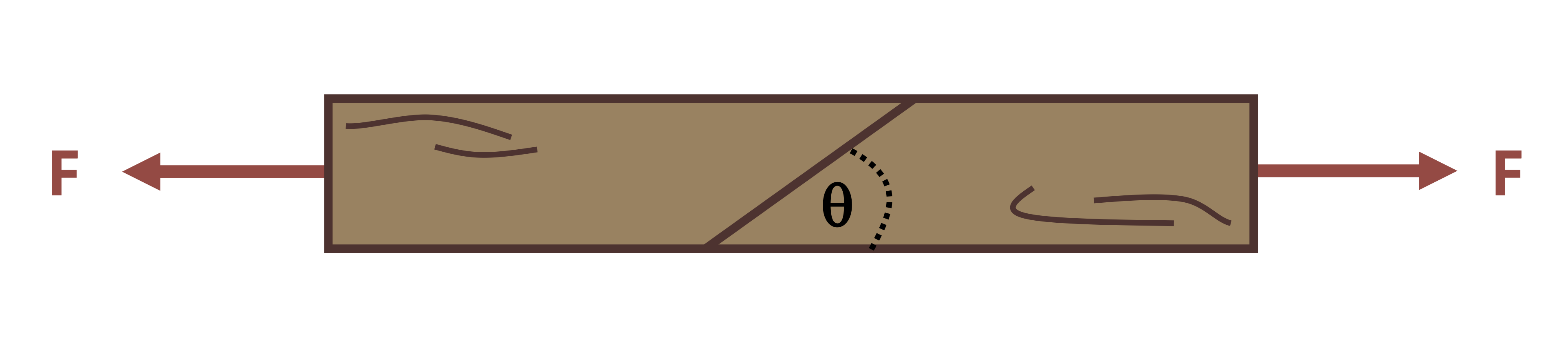
We have so far been cutting cross-sections perpendicular to the external force, or parallel to it. However, there is no rule that says we have to do this. It is perfectly acceptable to cut cross-sections at an angle and there are many situations where it may make sense to do so (Figure 2.7).
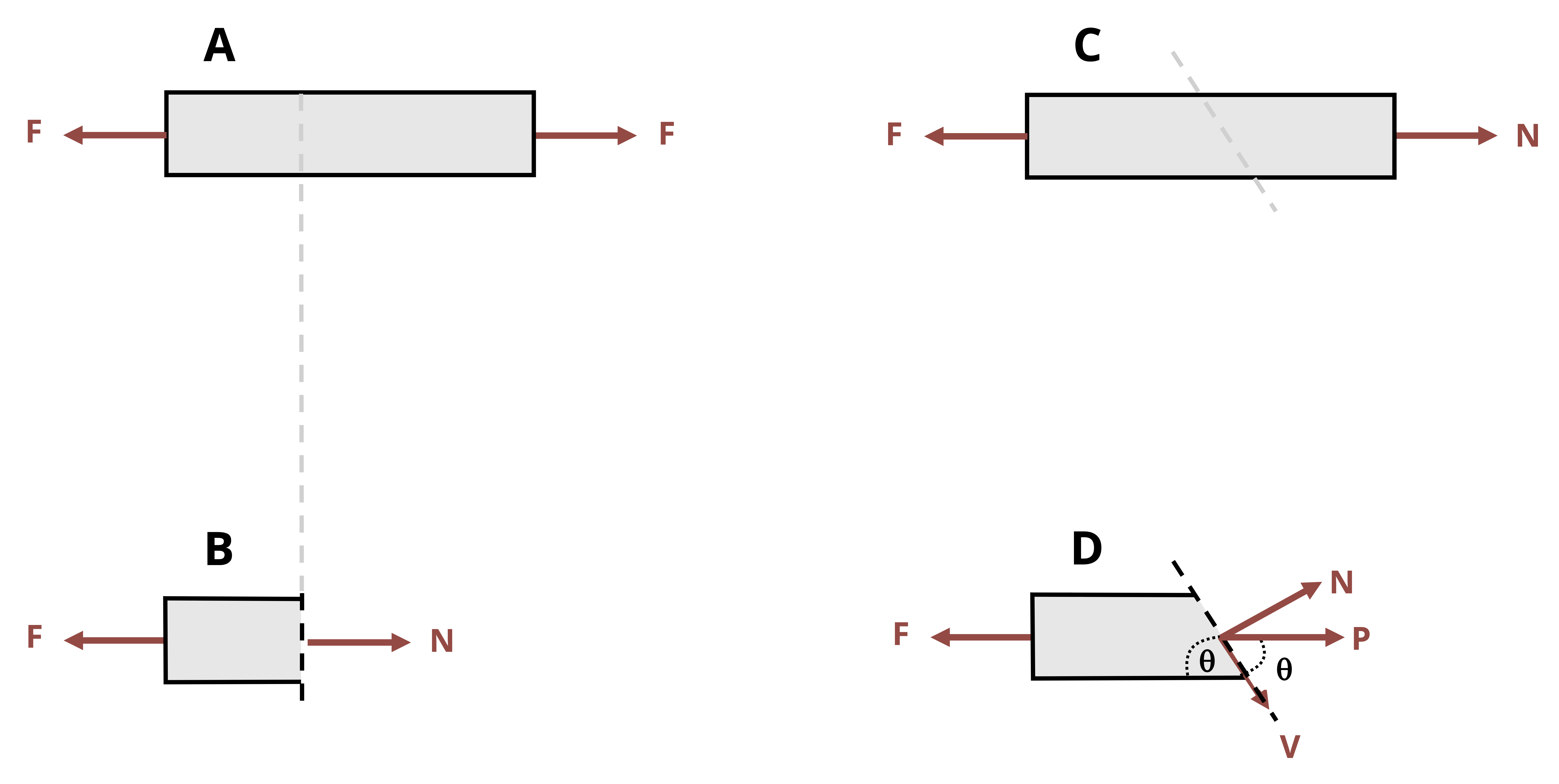
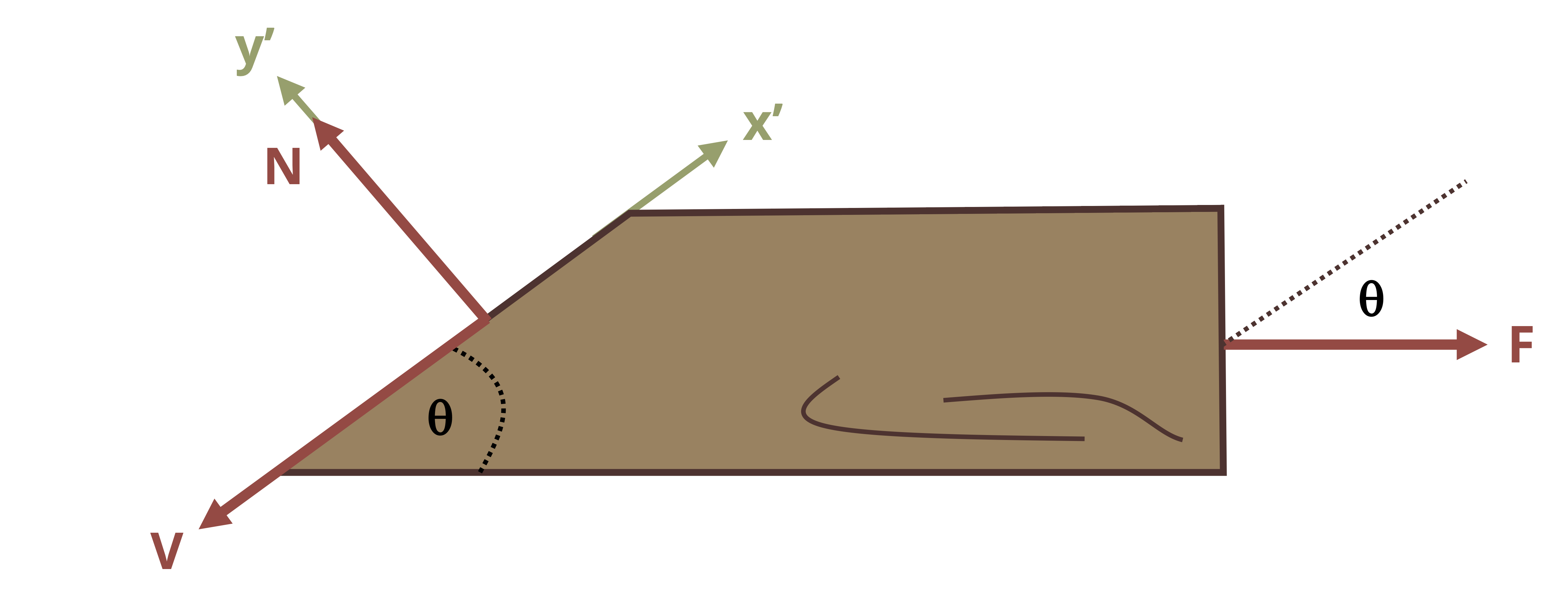
In this scenario the internal load must still be equal and opposite to the external load in order to maintain equilibrium but, because we cut the cross-section at an angle, this internal load is neither parallel nor perpendicular to the cross-section. Therefore it is not entirely a normal force or a shear force. However, the internal force may be broken into components that are perpendicular and parallel to the cross-section.
\[ \begin{aligned} & N=P \sin (\theta) \\ & V=P \cos (\theta) \end{aligned} \]
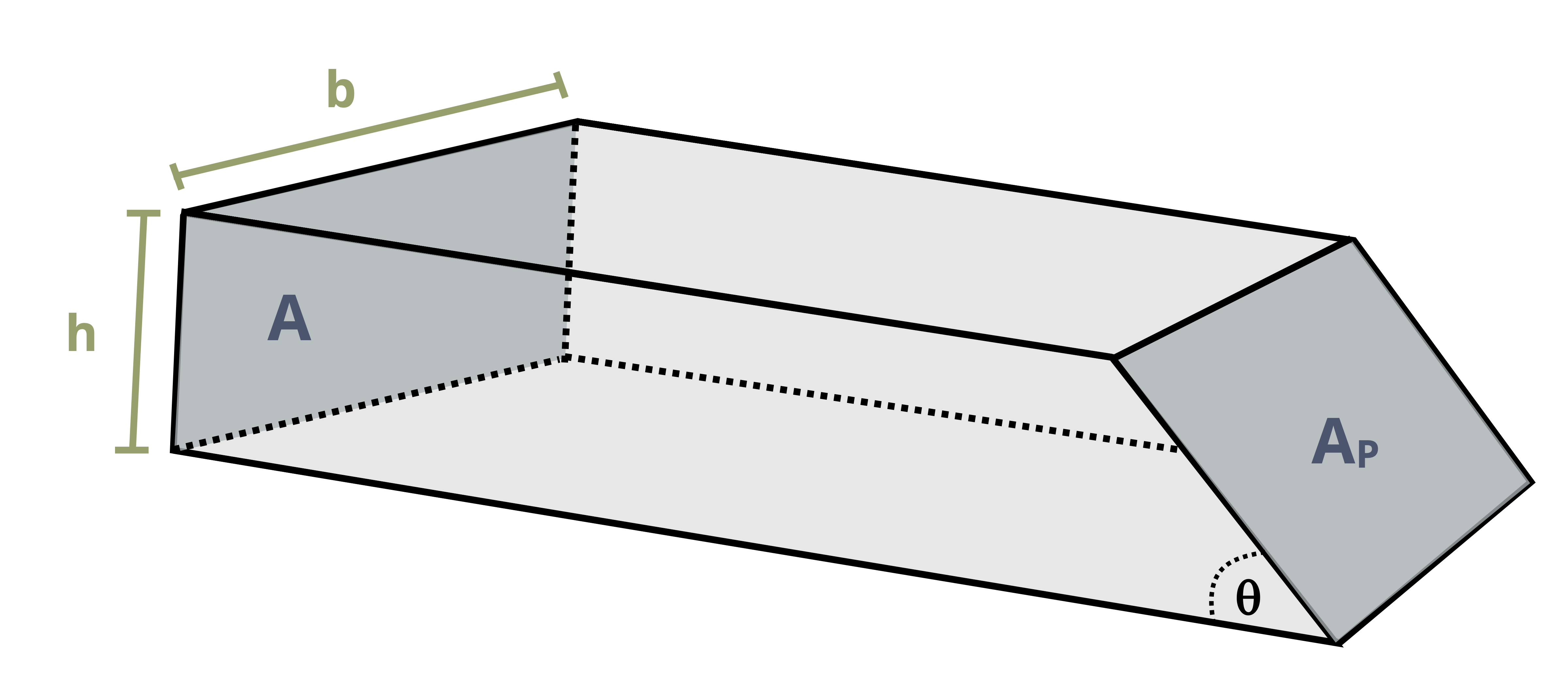
The area used to calculate the average normal and shear stresses must be the area of the inclined plane (Figure 2.8). By setting up a right-angled triangle it should be apparent that the area of the plane, Ap, can be found from:
\[ A_p=\frac{A}{\sin (\theta)} \]
We can calculate average normal stress from:
\[\boxed{\sigma=\frac{N}{A_p}=\frac{P \sin (\theta)}{\frac{A}{\sin (\theta)}}=\frac{P \sin ^2(\theta)}{A}} \tag{2.3}\]
We can calculate average shear stress from:
\[\boxed{\tau=\frac{V}{A_p}=\frac{P \cos (\theta)}{\frac{A}{\sin (\theta)}}=\frac{P \sin (\theta) \cos (\theta)}{A}} \tag{2.4}\]
𝜎 = Average normal stress on the inclined plane [Pa, psi]
τ = Average shear stress on the inclined plane [Pa, psi]
N = Internal normal force perpendicular to the inclined plane [N, lb]
V = Internal shear force perpendicular to the inclined plane [N, lb]
Ap = Area of the inclined plane [m2, in.2]
A = Cross-sectional area [m2, in2]
P = Internal load perpendicular to cross-sectional area A [N, lb]
𝜃 = Angle between the inclined plane and the axis perpendicular to cross-sectional area A [°]
Note these equations assume the angle (𝜃) is measured from the axis perpendicular to area A. For a horizontal beam, area A is in the vertical plane so angle θ is measured from the horizontal axis.
Even if the external load remains constant, we can obtain different values for the internal normal and shear forces (and therefore different values for the stresses) by changing the angle at which we cut the cross-section. We’ll explore the implications of this further in Chapter 12. For now, a demonstration of calculating the stresses on an inclined plane is given in Example 2.5.
Example 2.5
A beam is formed of two structural wooden members that are glued together along an inclined plane at angle θ = 40° and subjected to a tensile force of F = 30 kN. The height of the beam is 50 mm and its thickness is 20 mm. Determine the normal and shear stresses created along the inclined plane.
Begin by cutting a cross-section along the inclined plane and drawing a free body diagram. Remember to include the internal normal and shear forces perpendicular and parallel to the cross-section.
Use equilibrium equations to determine the internal forces. It will be easiest to define axes parallel and perpendicular to the inclined plane.
\[ \begin{aligned} \sum F_{x^{\prime}}= F \cos (\theta)-V=0 \\ \sum F_{y^{\prime}}= N-F \sin (\theta)=0 \end{aligned} \]
With F = 30 kN and θ = 40°, these can be solved for N = 19.3 kN and V = 23.0 kN.
Next, determine the cross-sectional area of the inclined plane.
\[ A_p=\frac{A}{\sin (\theta)} \]
With \(A = 0.05{~m}*0.02{~m} = 0.001{~m}^2\) and \(θ = 40°\), \(Ap = 0.00156{~m}^2\).
Finally, determine the average normal stress and the average shear stress.
\[ \begin{aligned} \sigma & =\frac{N}{A_p}=\frac{19,300{~N}}{0.00156{~m}^2}=12.4 \times 10^6 \frac{{N}}{m^2}=12.4{~MPa} \\ \tau & =\frac{V}{A_p}=\frac{23,000{~N}}{0.00156{~m}^2}=14.8 \times 10^6 \frac{\mathrm{N}}{m^2}=14.8{~MPa} \end{aligned} \]
Summary
Click to expand
References
Click to expand
Figures
Figure 2.1: Forces pulling on a cross-section cause tension, while forces pushing on a cross-section cause compression. Left image: Orangeaurochs. 2012. CC BY 2.0. https://flic.kr/p/dqmXdM. Right image: Unknown author. 2017. Public domain. https://pxhere.com/en/photo/993074. Diagrams: Kindred Grey. 2024. CC BY-NC-SA.
Figure 2.2: The internal load is equally distributed over the cross-sectional area, but may be represented as a single concentrated load acting at the center (N in this case). Kindred Grey. 2024. CC BY-NC-SA.
Example 2.1: Jbarta. 2010. CC BY-SA 3.0. https://en.wikipedia.org/wiki/File:Permanent-column-form.jpg.
Example 2.2: Kindred Grey. 2024. CC BY-NC-SA.
Figure 2.3: (a) External loads F creating (b) an internal normal force (N) perpendicular to the cross-section. Kindred Grey. 2024. CC BY-NC-SA.
Example 2.3: Kindred Grey. 2024. CC BY-NC-SA.
Figure 2.4: Pins experiencing (a) single shear and (b) double shear. Kindred Grey. 2024. CC BY-NC-SA.
Example 2.4: James Lord. 2024. CC BY-NC-SA.
Figure 2.5: Circular column sitting upon a rectangular foundation. Jiří Sedláček - Frettie. 2010. CC BY-SA 3.0. https://commons.wikimedia.org/wiki/File:Footing_of_column_in_collections_of_Muzeum_Vyso%C4%8Diny_in_T%C5%99eb%C3%AD%C4%8D,_T%C5%99eb%C3%AD%C4%8D_District.jpg.
Figure 2.6: When calculating the bearing stress between curved surfaces, project a rectangle of area A = d*t. Kindred Grey. 2024. CC BY-NC-SA.
Figure 2.7: (a) External loads, F, will create (b) an internal normal force, N, when a cross-section is cut vertically. Kindred Grey. 2024. CC BY-NC-SA.
Figure 2.8: When calculating the stresses on an inclined plane, it is important to use the area of the plane, Ap, rather than the area of the cross-sectional plane, A. Kindred Grey. 2024. CC BY-NC-SA.
Example 2.5: Kindred Grey. 2024. CC BY-NC-SA.